Learning Random Determinstic Finite Automata with Self-Attention
Figure 1: (Kevin Lang, 1998)
Author's Note: This is a lightly edited version of an early draft of a paper that I had worked on towards the end of grad school. All of the work was originally done prior to April of 2021, which is why it may sound a little anachronistic given the date it was uploaded.
Self-attention represents the backbone of many of the cutting-edge breakthroughs in machine learning. However, little is know about the theoretical qualities of self-attention based learning mechanisms. This installment attempts to shed some light on this area by evaluating the ability of transformers to passively learn deterministic finite automata (DFA). Over the course of 1700+ trials, we were able to determine direct predictive relationships between the underlying parameters of certain forms of DFAs and the performance of both self-attention and recurrence based models. Potentially more significant, we also demonstrate certain forms of DFA which are easily solved by small recurrent networks, but prove challenging for even advanced self-attention based models.
1. Background
From natural language processing to computer vision, transformers (Vaswani, Ashish and Shazeer, Noam and Parmar, Niki and Uszkoreit, Jakob and Jones, Llion and Gomez, Aidan N. and Kaiser, Lukasz and Polosukhin, Illia, 2017) have set state of the art performance on a wide variety of tasks. The key breakthrough behind this success is the attention operation. This method of modeling sequences has proved not only capable of developing high quality representations, but also very amenable an efficient scaling up of these models. Although attention and self-attention had existed in different forms previous to this architecture, the transformer was the first to claim that it was "all you need."
However, little is known about the theoretical learning properties of self-attention. There has been ample empirical work attempting to better understand how the performance of transformers scales with different key training hyperparameters, but these works often focus solely on language based datasets. Although this allows a better understanding of the practical use of transformers, it does not aid in understanding the fundamental relationship between task complexity and representational capacity for these models.
Figure 2: In practice, we know that bigger networks can represent more complex functions than smaller networks. But how much bigger? And how much more complex?
Deterministic finite automata (DFA) have been an area of active study in computational theory for decades. They represent a straight forward sequential modeling problem domain with well known complexity properties and easily modifiable hyperparameters. Importantly for our use case, they are easy to randomly generate and provide a straightforward evaluation methodology.
In this installment, we run a series of experiments evaluating the performance of different types of models at passively learning DFAs from samples. We will then try to connect the performance of these models to the underlying complexity of the DFA, and use this to extrapolate practical insights about the differences between the representational capacity self-attention based networks and recurrence based networks.
2. Background
There has been a good amount of work on the computational limits for standard recurrent neural networks. (H.T. Siegelmann and E.D. Sontag, 1995) demonstrated that these networks could theoretically simulate arbitrary Turing machines with enough compute. (Samuel A. Korsky and Robert C. Berwick, 2019) were able to show that certain realizable forms of RNN's were exactly as powerful as DFA's and, assuming arbitrary levels of precision, could be at most as powerful as pushdown automata.
A similar result for transformers was able to demonstrate that transformers with infinite parameters are as powerful as turing machines (Pérez, Jorge and Marinković, Javier and Barceló, Pablo, 2019). However realizable forms of transformers are known to be more limited. (Hahn, Michael, 2020) demonstrated that for every fixed size transformer, there exists a context-free grammar that it cannot express to a given level of accuracy for both hard and soft attention. Different forms of architectures have been proposed specifically to mitigate this non-universality, notably the universal transformer (Dehghani, Mostafa and Gouws, Stephan and Vinyals, Oriol and Uszkoreit, Jakob and Kaiser, Łukasz, 2018) which augments the standard transformer architecture with a form of recurrence similar to that of RNNs. However, most practical applications still opt to use a form of the standard transformer architecture.
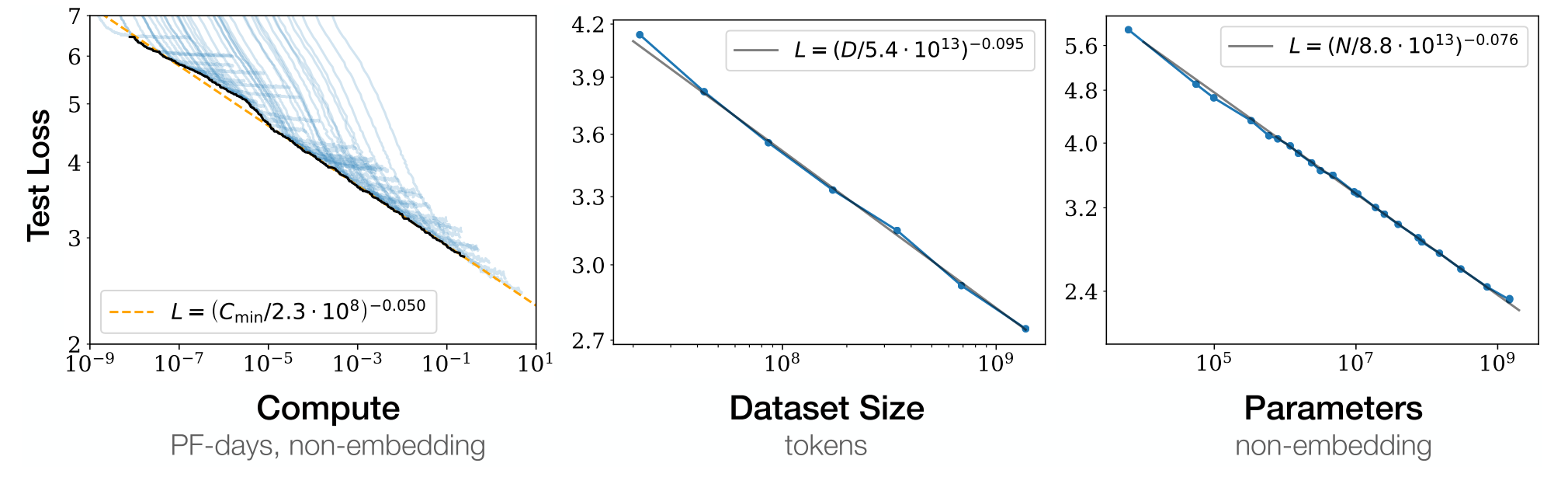
Figure 3: Graph from (Jared Kaplan and Sam McCandlish and Tom Henighan and Tom B. Brown and Benjamin Chess and Rewon Child and Scott Gray and Alec Radford and Jeffrey Wu and Dario Amodei, 2020)
There have been a large number of experiments to better understand the capabilities of transformers at scale. These works were mostly inspired by (Jared Kaplan and Sam McCandlish and Tom Henighan and Tom B. Brown and Benjamin Chess and Rewon Child and Scott Gray and Alec Radford and Jeffrey Wu and Dario Amodei, 2020), which was able to demonstrate that the overall performance of transformer-based language model was a surprisingly smooth power law in terms of some of the key training hyperparameters. Our work is in a similar vein to these works, however, we focus not only on modifying the underlying model but also modifying the complexity of the underlying dataset.
Exactly passively learning DFA's from samples is known to be as hard as cryptography. (Kearns, Michael and Valiant, Leslie, 1994) The experiments carried out in this paper are inspired by a similar set of experiments were carried out in (Kevin Lang, 1998). In this work, the authors were able to devise a direct predictive relationship between the hyperparameters of a certain subset of DFAs and the accuracy of an algorithm on passively learning that DFA. Our work seeks to discover a similar relationship for transformers.
There have been a few works looking at the specific connection between deep learning and finite automata. (William Merrill, 2019) introduces a set of theoretical tools for analyzing the ability for sequential neural networks to learn different kinds of formal languages. In (Gail Weiss and Yoav Goldberg and Eran Yahav, 2021), the authors develop a formal computational model behind the operations that a transformer is capable of. They use this model to then derive and experimentally validate bounds on the minimum architecture size required to learn different operations. There is also a good amount of work on using transformers to find approximate solutions to known NP-Hard problems, most notably the traveling salesman problem in (Kool, Wouter and van Hoof, Herke and Welling, Max, 2018) and (Xavier Bresson and Thomas Laurent, 2021).
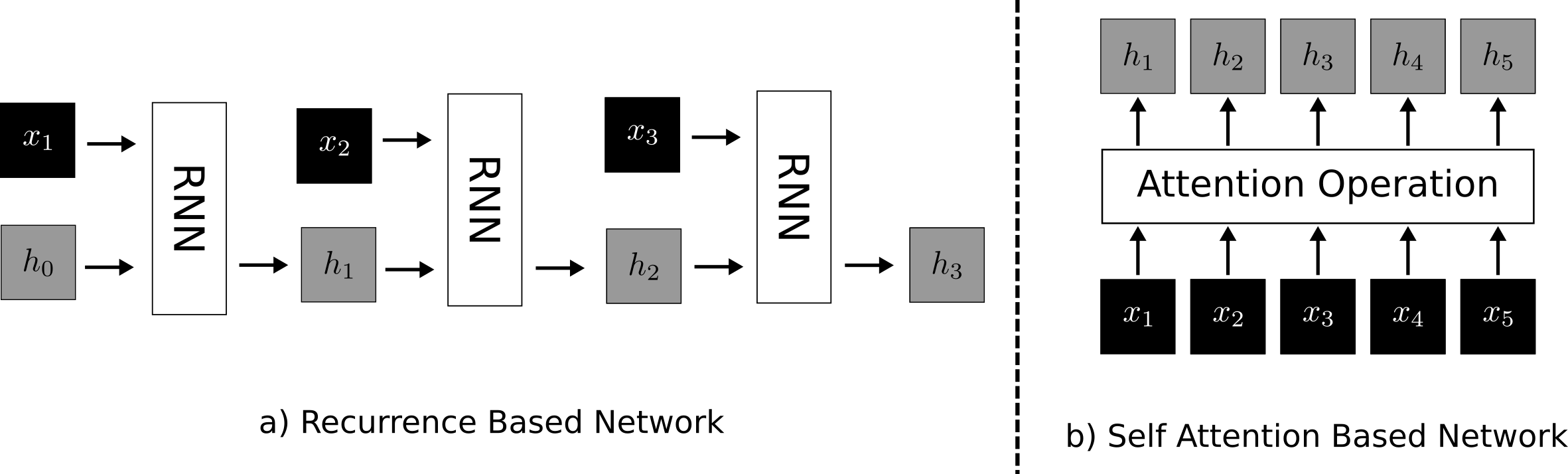
Figure 4: Visual comparison of a recurrence based and self-attention based architecture. The recurrence based architecture (a) processes each \(x\) in the sequence one by one. Every time it outputs a hidden state representation \(h_i\) for the corresponding \(x_i\). This is then fed into the network to compute \(h_{i + 1}\) for \(x_{i + 1}\). By continually passing the hidden state from the last computation to the next, the network can send information through time, allowing the representation for \(x_{i + 1}\) to depend on \(x_i\). Self attention (b) on the other hand computes all of the hidden states at once in a single feed forward operation. It effectively simulates sequential processing by constricting which parts of the sequence can attend to other parts of the sequence.
2.1. Recurrent Neural Networks
Recurrent neural networks pass sequential information through a recurrence relationship. Let's say we have a sequence of floating point vectors \(x_1, x_2, x_3, \dots, x_n\) and a predetermined hidden dimension \(d_h\). We would define our network as a function of two inputs, one for a data vector \(x_i\) and one for a hidden state \(h_{i-1}\). We would start by defining some constant parameter \(h_0\) of size \(d_h\). We would feed this into our network with our first data vector, \(x_1\) to get its corresponding \(h_1\). Then, we would feed this \(h_1\) back into our network again with \(x_2\) to get \(h_2\). We would then continue this chain until we reach \(x_n\). We can think this process as the recurrent application of our network \(f\) to itself and the data,
\begin{equation} h_n = f_n(x_n, f_{n-1}(x_{n-1}, f_{n-2}(x_{n-2}, \dots f_2(x_2, f_1(x_1, h_0)))\dots ) \end{equation}hence the name "recurrent neural network." This process is visualized figure 4.
These kinds of networks were the workhorse of natural language processing for many years, with many different architectural variations on this underlying theme. There are clear functional analogies between recurrent neural networks and the processing mechanisms of turing machines or pushdown automata. Each of these operates as a function that reads in some state, updates its internal state, and continues processing. This similarity in the underlying computational framework has made theoretical connections between RNN's and other computational learning theory concepts relatively straightforward.
2.2. Self Attention
Models using self attention process sequential data in a fundamentally different manner. Instead processing the sequence sequentially, everything happens in parallel. There is no fixed order that they process the data, the representations for each object is computed at the same time. For each \(x_i\), we compute three different vectors: a query vector \(q_i\), a key vector \(k_i\) and a value vector \(v_i\). We compute \(h_i\) by first doing a scaled dot product between \(q_i\) and all the other key values: \(k_1,k_2,\dots,k_n\). For stability, this result is often scaled by a factor of \(\frac{1}{\sqrt{d}}\), where \(d\) is the size of the vector dimension. The dot product values are then put through a softmax activation which scales them such that they are all between 0 and 1, and then sum to one. The \(h_i\) is then computed using as weights for a weighted sum of all of the value vectors.
Written out in matrix notation,
\begin{equation} \text{Attention}(Q, K, V) = \text{softmax}(\frac{QK^T}{\sqrt{d}}) V \end{equation}where Q is a matrix containing all of the query vectors, K is a matrix containing all of the key vectors, and V is a matrix containing the value vectors. This is the underlying attention mechanism. When the queries, keys and values are all coming from the same set of vectors, it is known as self-attention. This processes is visualized in figure 4.
This operation alone is notably not sequential, meaning it has no understanding of the relative ordering of each \(x_i\) as it is computing its representation. In order to account for this ordering, most models will incorporate a form of "positional encoding", where the sequence information is converted to a vectorized form and then added to the underlying data vector, \(x_i\). Meaning, every \(x_i\) has an additional vector that encodes the index number \(i\) added to it. This allows the model to learn the relationships between the input positions, rather than treating them in a fixed manner.
3. Experiments
For our experiments, we trained a series of models on the task of predicting whether or not a string was accepted by a particular finite automata. We generated static datasets of strings of 21 symbols and treated the problem like a supervised learning task. For all of the models, we held the total number of iterations and batch sized fixed, to allow a direct comparison between them.
For our main models, we used a series of transformer models with 2, 4, and 8 layers self-attention respectively, Each had an internal hidden dimension of 128. These models implement the vanilla form of self-attention described above, closest to the version introduced in the original paper (Vaswani, Ashish and Shazeer, Noam and Parmar, Niki and Uszkoreit, Jakob and Jones, Llion and Gomez, Aidan N. and Kaiser, Lukasz and Polosukhin, Illia, 2017). Our hope was to keep the underlying architecture as simple as possible, to isolate the specific effects of self-attention and not further optimizations.
3.1. Random Trellis Machines
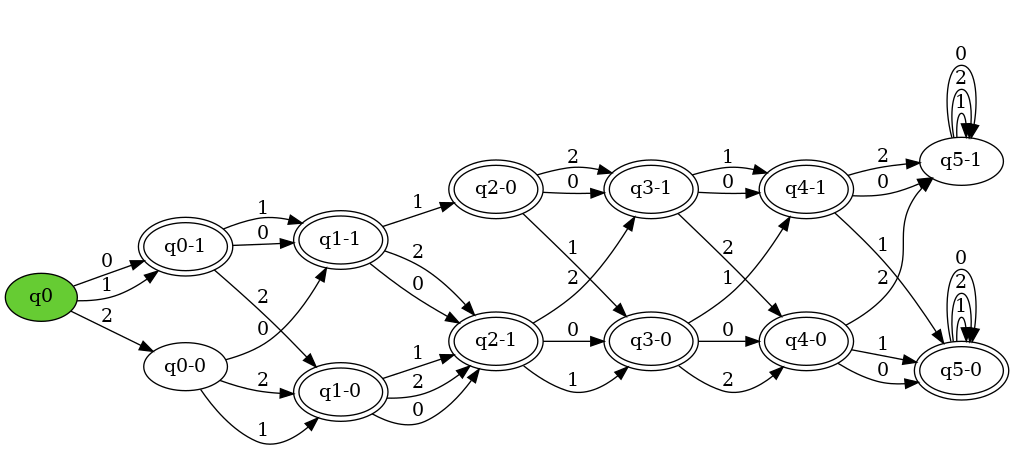
Figure 5: Example of a trellis machine with width 2, depth 6, and alphabet size of 3
This set of experiments deals with a subset of deterministic finite automata known as trellis machines. These are DFA's with a unique feed-forward structure. They are composed a series of layers of nodes of a fixed width. Each layer can only be connected to adjacent layers. Figure 5 contains an example of a trellis machine.
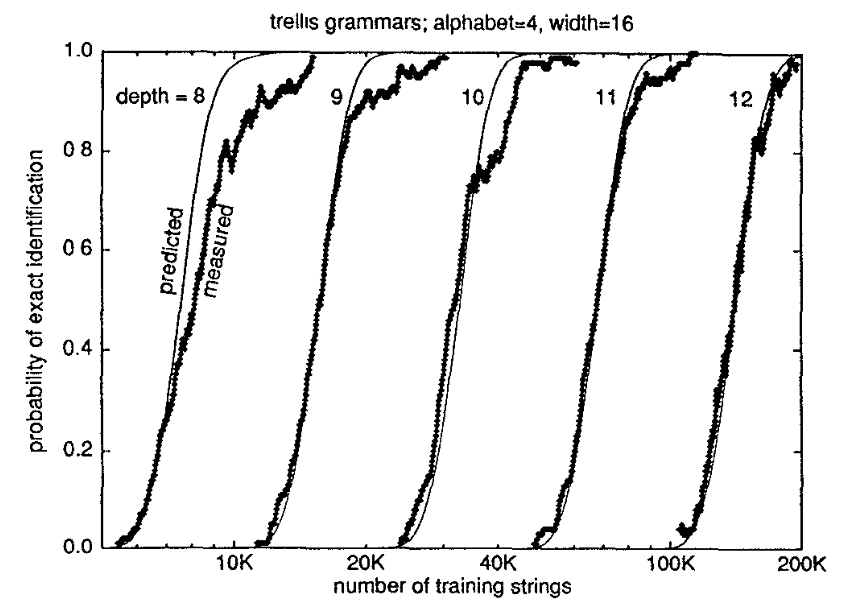
Figure 6: Sample of the analysis from (Kevin Lang, 1998)
In (Kevin Lang, 1998), they were able to derive the following relationship between the parameters of the trellis machine and the number of examples to reach a desired level of performance for their algorithm as,
\begin{equation} \text{Examples}(a, w, d) = O\left(\left( \frac{a w}{w - 1} \right)^{d/2}\right) \end{equation}where \(a\) is the alphabet size, \(w\) is the width and \(d\) is the depth. For these experiments, we want to see if we can develop a similar understanding of the relationships between the parameters and the performance of our models. Although the bounds cited above are for a specific algorithm, we want to compare and contrast the learning properties of these general purpose sequence learning models to the DFA-specific algorithm. However, since modifying the depth changes the total size of the dataset and therefore makes comparisons between models less clear, we opt to only study the scaling properties of width and alphabet size.
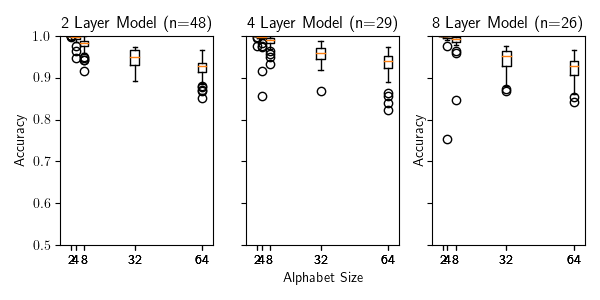
Figure 7: Performance of the baseline transformer models on trellis machines with scaling alphabet sizes. In this figure and all following figures, n represents the minimum number of samples for any of the settings. Meaning that in the above figure, each alphabet size had at least 26 samples for the 8 layer model.
Our first set of experiments dealt with the size of the underlying alphabet. We started with a width of 2, depth of 21 and an alphabet size of 2. We then iteratively doubled the alphabet size until it reached 64. At every size, we trained a series of our baseline transformer models for a single epoch over our data, and then measured their accuracy on the test set. Their performance is shown in figure 7.
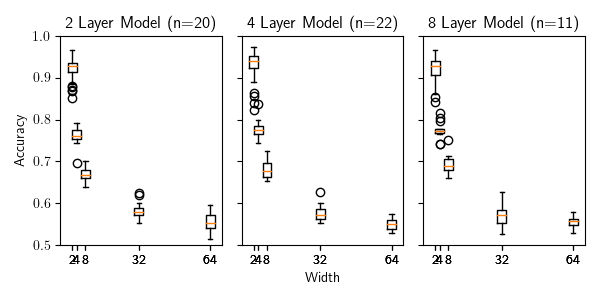
Figure 8: Performance of the baseline transformer models on trellis machines with scaling widths
We then repeated a similar experiment for the width of the trellis machine. This time, we started with a trellis machine of width 2, depth 21, and alphabet size of 64. We then continually doubled the width until it reached 64. We trained an identical set of models using identical hyperparameters. The performance of these models is shown on figure 8.
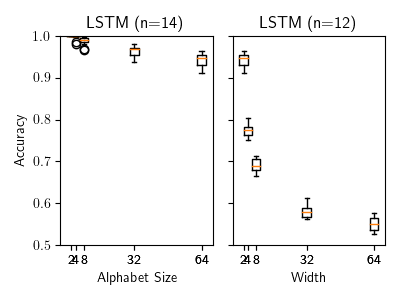
Figure 9: Performance of the LSTM model at the scaling tasks
To better understand how much of this pattern has to do with self attention in particular, we also ran these experiments with a simple LSTM (Hochreiter, Sepp and Schmidhuber, Jürgen, 1997) model with 6 layers and a hidden dimension of 128. The results for this model closely resembled the performance of the transformer based models, and can be seen in figure 9. This suggests that performance on trellis machines does not distinguish the self-attention based and recurrence based models.
3.2. Random DFAs
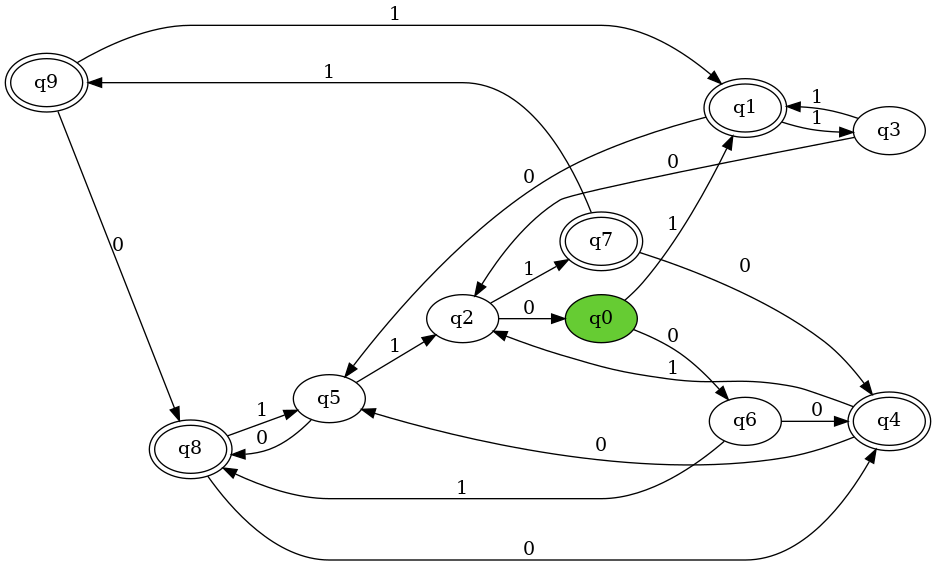
Figure 10: Example of a randomly generated DFA with 10 states
We generated fully random DFAs with a simple algorithm. For every node, iterate over all of the symbols in the alphabet and randomly created an edge with that symbol to another node. Every node was given a 50% chance of being an acceptance node. We generated all \(2^{21}\) possible binary strings, and randomly split these into a train and test sets. We assigned every string a binary label, indicating whether or not it was accepted by the DFA. To avoid any degenerate cases (accepting almost everything or nothing), we ensure that every generated DFA had an acceptance rate between 45%-55%. We noticed in earlier versions of this experiment that much of the noise in the outcome could be attributed to the odds of generating an underlying acceptance rate (0% or 100%) that was trivial to imitate. An example of a generated dfa can be seen in figure 10.
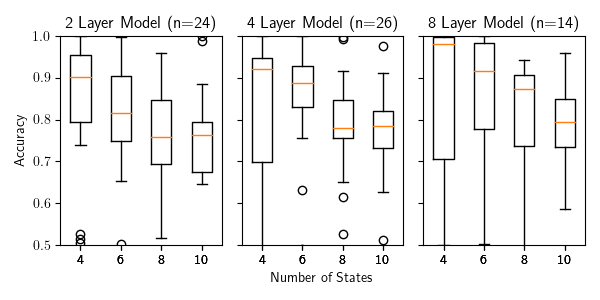
Figure 11: Performance of the baseline transformer models on randomly generated DFA with 10 states
Figure 11 demonstrates the performance of our transformer models on randomly sampled DFA's of size 4, 6, 8, and 10. You'll notice that these models perform surprisingly poorly on this task, with even the largest model consistently failing to learn some of the small DFA's.
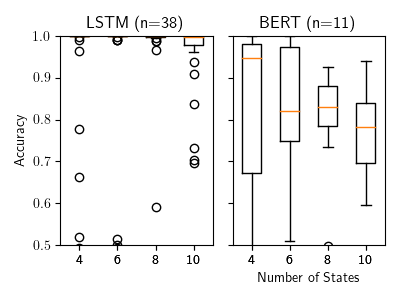
Figure 12: Performance of the additional models on randomly generated DFA
As a comparison and validation step, we also evaluated two additional models representing the opposite ends of the spectrum. The first was the LSTM model used in the previous experiments. The second was a miniaturized version of BERT (Devlin, Jacob and Chang, Ming-Wei and Lee, Kenton and Toutanova, Kristina, 2018) with a hidden size of 768 and two hidden layers. This model is a state-of-the-art language model used in text classification tasks.
Figure 12 demonstrates their performance. BERT performs similarly to the baseline transformer models, giving supporting evidence to the idea that we are seeing a general property of self-attention based models and not a result of our implementation. Somewhat surprisingly in comparison, the LSTM does not have any difficulty with this task whatsoever, reaching near perfect performance on each of number of states. It is worthwhile to mention that in (Kevin Lang, 1998), the authors were getting better performance with their algorithm using randomized DFAs with much more complex configurations. This further emphasizes how poorly these transformers are performing at this task.
4. Analysis & Discussion
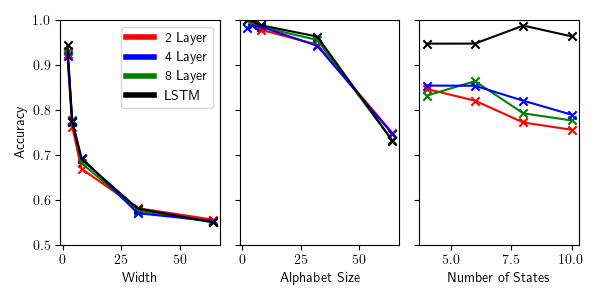
Figure 13: Comparison of the mean accuracy values across the different size transformers and LSTM.
Figure 13 contains the plot summarizing the mean performance for the models across the different tasks. The key takeaways from these experiments are summarized as follows.
Transformers perform poorly at learning random DFA. The transformer based models performed surprisingly poorly at this task, especially considering the performance of the LSTM model. Transformers models are known to handle hierarchy and cyclical patterns relatively poorly (Hahn, Michael, 2020), so it is possible that these small DFAs end up exacerbating those issues. However, this failure points to obvious room for future improvement for these types of models.
It also points to an interesting area of further study. The fact that the transformer models struggle with these cyclical networks, but perform well in practice should shed some insights on the types of structures that language-based modeling networks need to be good at. An interesting future analysis may try to attempt this process in reverse: attempting to find the DFA structures that transformers perform the best on, and analyzing how these align with natural language. This could potentially be a powerful framework for architecture design. By evaluating the performance of the model on small intelligently crafted DFAs, we could potentially extrapolate their performance generally on language based tasks.
Model performance on trellis machines degrades roughly linearly with alphabet size and roughly exponentially with width. This result was particularly interesting since there was not a strong indication of how the model would scale with respect to either of these parameters. These results indicate a different behavior than in (Kevin Lang, 1998), which is not surprising given how different the two algorithms are. It suggests that these models are close to the optimal level of efficiency for handling increases in the size of the alphabet, but struggle with increasing the width. This is especially interesting since this pattern extended consistently across all the model sizes and types.
This potentially offers some practical insights in terms of designing tokenization strategies for transformer networks. For example, DNA sequences can be represented by a series of nucleotides (i.e. representing AGTATC as ["A", "G", "T", "A", "T", "C"]) or as "k-mers" (i.e. representing AGTATC as ["AGT", "ATC"]). We can think of these structurally as two different automata that accept the same language, but with different size alphabets and states. For any non-natural language, practitioners need to craft a vocabulary and syntax entirely from scratch. Each language will have different possible representations that will lead to different levels of performance.
Network size did not seem to have an effect. Interestingly the size of the network itself did not seem to be correlated at all with performance, even with our largest model being four times the size of the smallest. In order to better investigate the effects of the size of the networks, it would be interesting to scale up the experiments such that we see a benefit from the larger models. Intuitively, larger networks should be able to learn to represent larger DFAs. Better understanding this relationship would be a valuable contribution to the study of scaling laws.
5. Conclusion
The shift to self-attention based learning mechanisms in natural language processing represented a radical departure from the previous recurrence based networks. Although we have seen significant increases in performance on a wide variety of tasks since this switch, the reasons why are still poorly understood. In this work, we attempted a series of experiments that were designed to help shed some light on the representational capacity of these two different types of networks. We were able to determine that the performance of recurrence based and transformer based models identically scale with complexity for a subset of DFAs known as trellis machines. However, we ended up only discovering DFA's in which self-attention based models perform worse than recurrence based models. We hope that these results represent an incremental step forward in terms of understanding not only what types of problems self-attention is well suited for, but also what types of problems might correlate with real world language modeling performance.
6. Bibliography
Dehghani, Mostafa and Gouws, Stephan and Vinyals, Oriol and Uszkoreit, Jakob and Kaiser, Łukasz (2018). Universal Transformers, arXiv.
Devlin, Jacob and Chang, Ming-Wei and Lee, Kenton and Toutanova, Kristina (2018). BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding, arXiv.
Gail Weiss and Yoav Goldberg and Eran Yahav (2021). Thinking Like Transformers, CoRR.
Hahn, Michael (2020). {Theoretical Limitations of Self-Attention in Neural Sequence Models}, Transactions of the Association for Computational Linguistics.
Hochreiter, Sepp and Schmidhuber, Jürgen (1997). Long Short-term Memory, Neural computation.
H.T. Siegelmann and E.D. Sontag (1995). On the Computational Power of Neural Nets, Journal of Computer and System Sciences.
Jared Kaplan and Sam McCandlish and Tom Henighan and Tom B. Brown and Benjamin Chess and Rewon Child and Scott Gray and Alec Radford and Jeffrey Wu and Dario Amodei (2020). Scaling Laws for Neural Language Models, CoRR.
Kearns, Michael and Valiant, Leslie (1994). Cryptographic Limitations on Learning Boolean Formulae and Finite Automata, Association for Computing Machinery.
Kevin Lang (1998). Random DFA's can be Approximately Learned from Sparse Uniform Examples.
Kool, Wouter and van Hoof, Herke and Welling, Max (2018). Attention, Learn to Solve Routing Problems!, arXiv.
Pérez, Jorge and Marinković, Javier and Barceló, Pablo (2019). On the Turing Completeness of Modern Neural Network Architectures, arXiv.
Samuel A. Korsky and Robert C. Berwick (2019). On the Computational Power of RNNs, CoRR.
Vaswani, Ashish and Shazeer, Noam and Parmar, Niki and Uszkoreit, Jakob and Jones, Llion and Gomez, Aidan N. and Kaiser, Lukasz and Polosukhin, Illia (2017). Attention Is All You Need, arXiv.
William Merrill (2019). Sequential Neural Networks as Automata, CoRR.
Xavier Bresson and Thomas Laurent (2021). The Transformer Network for the Traveling Salesman Problem, CoRR.