Dominoes

Figure 1: Image by DALLE 2
It is hard to imagine a simpler game to play than Dominoes. It tests the type of skills you are expected to master prior to entering pre-school: colors, shapes, counting and so on. But behind this game's simple surface lies a somewhat surprising tangle of complexity. In practice, it turns out there is a clear dividing line between the version of dominoes that is easily solvable with a laptop and the version we cannot solve with a supercomputer. That line is determined by the number of players: four players is solvable, three is not.
In this installment I am going to talk about building a domino "solver", covering:
- Whether an polynomial time optimal solver exists (No)
- Whether this matters in pratice (Not really)
- How this effects who ends up winning
What is Dominoes?
There are many different forms of the game dominoes, but each follows the same simple mechanics. Each domino is a tile that has two numbers on it. There is an initial pool of dominoes of a fixed size. Normally, this is a set of all unique combinations of two numbers from 0 to 12, known as "double twelves". Players are given a pile from this pool. You form chains by aligning tiles based on their numbers. The goal is to make the best possible chain.

Figure 2: A sample chain with its corresponding score. The 0, 0 domino here is the starting piece drawn initially.
The formulation that we will be talking about involves each player trying to form their own chain. A double-sided domino (meaning, one that has the same number on both sides) will be initially drawn to form the base of each chain. The remaining pile of dominoes is evenly distributed among the players. Players then start from this initial domino and make the longest chain they possibly can with their tiles. The exact rules of how this proceeds is not super relevant, but the eventual winner is the player who ends up with the lowest total sum of numbers on their remaining tiles. The goal then is for each player to make the chain that uses up the greatest amount of points from their initial pile.
Thinking About an Optimal Solution
The core optimization problem is as follows: given a set of dominoes, what is the chain with the largest sum of numbers on its tiles? Let's start by thinking of the brute force case, enumerating all of the possible chains and selecting the best one. With \(n\) dominoes, you can in theory make a grand total of \(n!\) different chains based on simple combinatorics. For every chain, we have \(n\) possible selections for the first domino, \(n - 1\) selections for the second and so on. This gives us \(n * (n - 1) * (n - 2) * ... 1 = n!\) possible chains.
We can immediately cut this down a good bit by thinking about the structure of the game. Although we may have up to \(n - 1\) choices for the second domino, in reality it will depend on the second number on the first tile. In a way, it has a structure similar to a search tree. We start out with an initial node corresponding to whatever the starting tile is. Every possible continuation of the chain becomes a child of this node and so on. Every single path through the tree represents a valid chain of dominoes.

Figure 3: Visualization of the Tree Structure. Each node is a decison point between the next possible piece to play.
Thinking about this a little bit further will allow us to update our bounds a bit. Each node can have at most 12 children, since there are only 13 tiles for every possible number and one is already in the chain. This allows us to revise our bound slightly to \(12^n\). 1
This formulation makes the algorithmic goal more clear. We need to search over all of the possible chains to find the chain that uses the most points. However, there is a slightly less obvious but more insightful structure we can use to think about the problem. Instead of thinking about trees, we can represent a pile of dominoes as a undirected graph. Each node represents a numeric "state" the chain can be in, and every domino is an edge between these nodes.
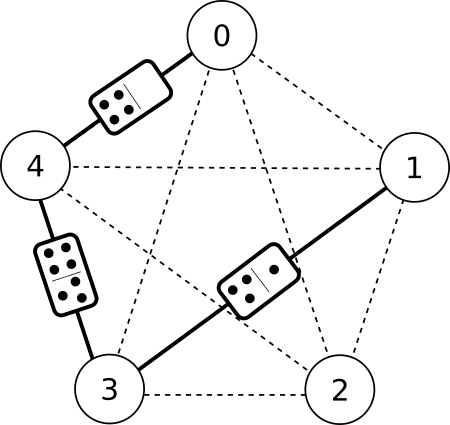
Figure 4: Visualization of the Undirected Graph Structure. Also, accidentally, a pentagram.
Finding a perfect path of dominoes would then be akin to finding a traversal of this graph that use every edge exactly once. You would start at the node corresponding to the initial number. Every edge coming off of this node would be a domino that has this number on it. Selecting an edge would then be akin to adding the corresponding domino to your chain. You then move to the next node connected to this edge, which will represent the number you must play next. To prevent using tiles in a chain more than once, you must remove the selected edge from the graph before continuing. You keep removing edges in this fashion until (ideally) there are none left.
There is a special name for this kind of path: an Eulerian Path. There is a polynomial time algorithm for both checking if one of these path exists and finding what that path is.
This does not mean there is a polynomial time algorithm for finding the best path. What if no perfect path that uses every edge exists? Well, there is a name for this problem as well: the longest path problem. If you are not familiar with graph theory, it might surprise you to learn that this problem is NP-Hard. But its true, there is no polynomial time algorithm that will find the optimal path.
This gives domino chain solving the following interesting property: there exists a polynomial time algorithm that tells us whether or not the problem is solvable in polynomial time. If this algorithmic check fails, then we are faced with an NP-Hard problem.
For a more in depth analysis of the theoretical computational complexity of dominoes, I highly recommend "Playing Dominoes is Hard, Except By Yourself."
Creating a Solver in Practice
There is no hope for a general polynomial time algorithm. This does not mean we are necessarily out of luck. Computational complexity tells us how the problem difficulty scales as we add more dominoes. However, the maximum number of dominoes you would ever need to consider is bounded. The most you can ever actually have in a pile is a modest 45. This would correspond to playing double-twelves in an intimate one-on-one setting. We can try to get a feel for the shape of the problem in practice via some simulations.
| Players | Max Starting Tiles |
|---|---|
| 2 | 45 |
| 3 | 30 |
| 4 | 23 |
| 5 | 18 |
| 6 | 15 |
The first thing we can get a feel for is just how common of an occurrence it is to have a perfect chain. To do so, we can just sample a bunch of randomized starting chains of different sizes and see how many have a perfect chain within them using our polynomial time checking procedure for an eulerian path.
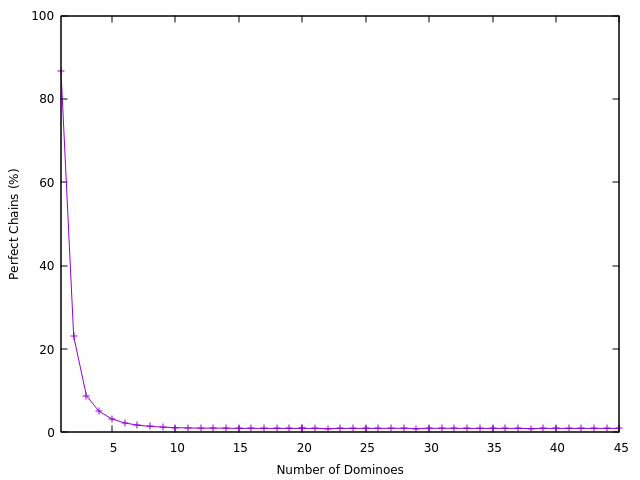
Figure 5: Empirical estimates of the probability of recieving a pile with a potential perfect chain.
Not that common apparently. We will only be able to run the polynomial solving algorithm around one percent of the time.
The next thing we want to check is just how hard of a search problem it is at the scales encountered in practice. We can do that by again sampling random starting chains and computing some statistics about the sizes of these search trees.
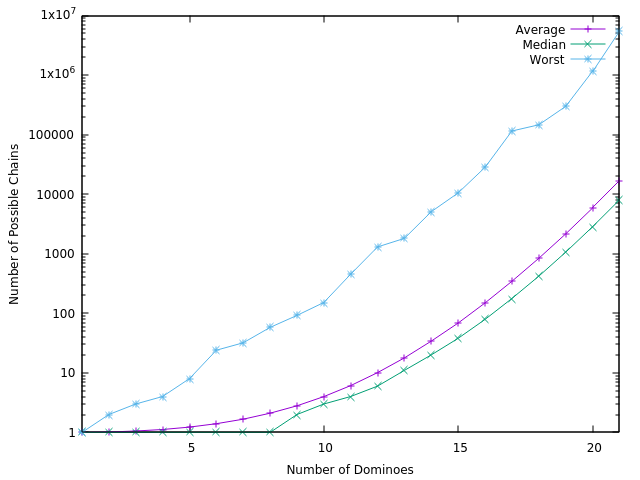
Figure 6: Empirical estimates of the the size of the search trees
This tells us a few things. First, it confirms the theoretical analysis from before. The y-axis on this graph is on a log scale and the number of possible chains is still growing exponentially. This is a nasty search space. Second, we can see that the worst case measured four player search space is somewhere between 100,000 and 1,000,000 possible paths. We can easily search over a few million possible combinations in a few seconds, even on limited computer hardware. This means that practically, generating solutions for four players is relatively trivial.
The issue then comes as we try to go from four players to three players, or from 23 dominoes to 30. A rough estimate from fitting a simple function to the data is that the average pile of 30 dominoes has about \(10^{15}\), or 1000 trillion possible paths. In other words, if you could search a billion paths a second, it would take 11 days to exhaustively search all possible options. Those seven dominoes between three and four players represent a computational cavern that we cannot cross. Since we determined that this game is NP-Hard, we cannot be saved by clever algorithms or heuristics either. This is a fundamental boundary which would only be resolved by showing that P=NP.
How Does This Effect Winning?
Before closing, it is worth considering how much this really matters in terms of winning the game. How much does finding the optimal solution even matter really?
Dominoes is a game with a lot of built in randomness. A player playing optimally will always have an edge on players playing non-optimally, but this edge might get drowned out at small sample sizes. We can try to estimate this a little bit by comparing two algorithms: a brute force algorithm that finds the optimal solution and a random algorithm that simply samples a fixed number of possible options and selects the best. This random algorithm has the nice attribute that it allows us to control the amount of compute used by adjusting the number of paths it samples.
Here we look at five versions of the random algorithm: sampling 1, 10, 100, 1000 and 10,000 possible chains. We compute the win rate of these algorithms against an optimal player for a number of dominoes corresponding to having between 4 and 8 players. As an example, four players here means that the random algorithm and the optimal algorithm both receive 23 dominoes, but they are still only compared in a head to head manner. Since the optimal algorithm is by definition optimal, the random algorithm can never achieve a true win rate above 50%.
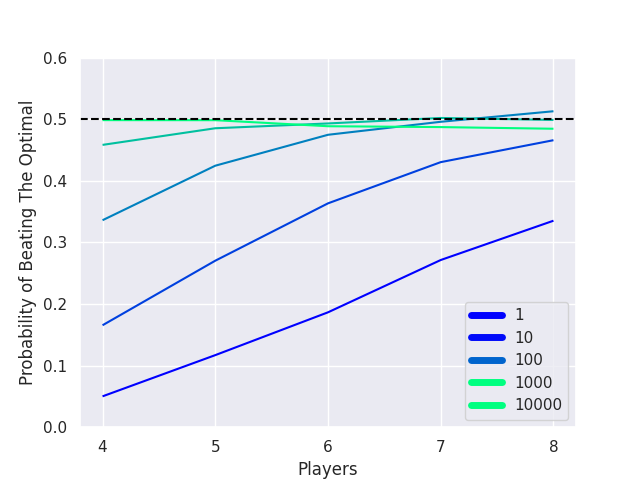
Figure 7: Win Rate Comparison
As you can see from the above graph, it takes roughly 10,000 random samples to closely re-create the odds of winning as optimal at four players. However, just randomly sampling a single valid chain always has a non-negligible probability of winning. As the number of players increases the gap between randomly sampling a single chain and all other algorithms decreases.
One last interesting thing to note from analyzing the above data is that the expected number of points remaining outside of the chain is not increasing as the player receives more pieces. In fact it peaks around 11 dominoes then decreases.
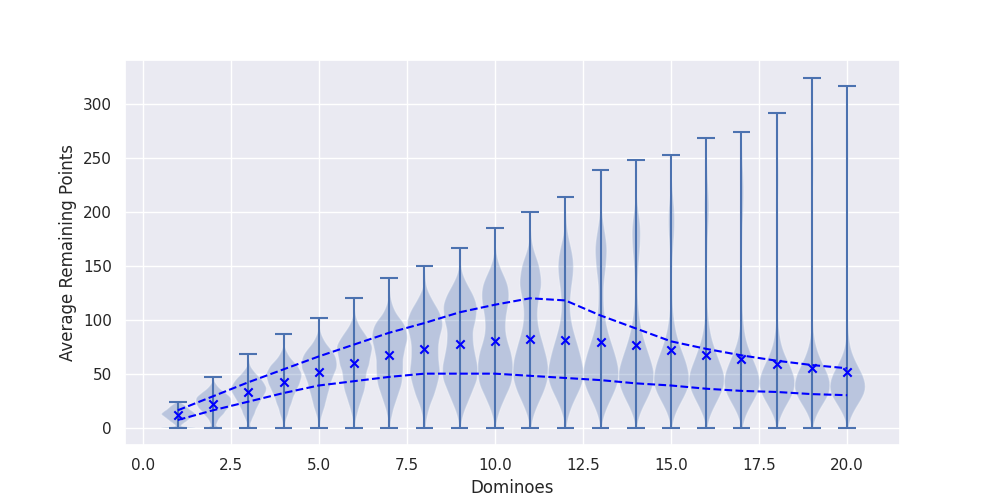
Figure 8: Average remaining point distribution for different sized piles. The x's represent the mean, and the lines correspond to the 50% interval.
Usually when the number of dominoes in the pile is not evenly divisible by the number of players, the extra dominoes are assigned to the players in a rotating fashion. This is normally viewed as a penalty, but in fact the opposite is true. For the standard amounts of players, adding an additional domino decreases the expected number of points remaining after you build your chain rather than increasing it. Having that additional domino is an advantage.
Conclusion
Applying a quantitative analysis to a game like dominoes might seem unnecessary. And for the most part, it is. This is a game meant for grandchildren to play with their grandparents. But often times when you dig a little deeper into these fun, simple games that have stood the test of time, you don't find clean, easy to solve equations. You instead find that many of the games we play are actually hiding a lot behind their humble exterior. In fact, I think it only leads us to appreciate these simple things a little more.
Footnotes:
: If you're a real stickler for details we can go even further and use that fact that the number of children is bounded by either 12 or the total number of remaining dominoes, whichever is smaller. If n \(\ge\) 12, then the bound is \(12^{n - 12} + 12!\) otherwise its \(n!\). But, that is a very clunky formula that only a stickler would love. You aren't a stickler are you?